クローズアップレンズ、というものがあります。カメラレンズの先端に取り付けると、物体により近づいて大きく撮影できるというアクセサリーですね。
小さなモノを撮りたい場合、レンズ交換式カメラではマクロレンズを使用するのが正攻法ですが、マクロレンズは高価です(マクロレンズが高価というより、交換レンズが高価といった方がいいかもしれません)。それに対して、クローズアップレンズは単純な凸レンズですので交換レンズに比べると格段に安く、1000~数千円程度で購入できるものがほとんどです。
もちろん、昆虫や花などをメインに撮影される方であればマクロレンズの購入をお勧めします。しかし、頻度は高くないけどマクロ撮影をやってみたい、どうしても資金が捻出できないのでクローズアップレンズで代用したい、と迷う人も多いはずです。
今回はそこにまじめに切り込んでみようと思います。第1回はクローズアップレンズの特性を光学的に考えてみます。(クローズアップレンズでどのぐらい像が劣化するのかという光学特性の解析ではありません。)
長文です。本記事の内容をWEB上で使える計算ツールとして公開しましたので、読みたくない方はこちらのツールをご利用ください。

どれ買えばいいのかわからん問題
クローズアップレンズはその強さに応じて番号が振られていて、クローズアップレンズNo.1~5、No.10というものもあります。誰が決めたか知りませんが、No.1が焦点距離1000mm、No.2が500mm・・・、No.10が100mmということになっています(追記:ディオプターですね)。しかし、問題なのは
どの番号のモノを買えばいいのかメーカーもはっきり言わない
ということです。国内メーカーで言えば、ケンコー、マルミ等がクローズアップレンズを販売していますが、どちらのサイトを見ても抽象的なことしか書いておらず(*)、自分のレンズにどのクローズアップレンズを付けたらどうなるか教えてくれません。クローズアップレンズ装着時に最大撮影倍率や最短撮影距離などがどうなるかはマスターレンズ側の設計に寄ってしまうのですべての組み合わせについて網羅できないからです。その他のブログにしてもしかりで、たまたま自分の持っているレンズでの使用例が掲載されていればよいのですが、組み合わせは無数にあるので大抵は参考になりません。
クローズアップレンズを買おうと思っている人は
- 自分のレンズでどれだけ近寄れるのか
- 最大撮影倍率はどこまであがるのか
といったことが知りたいはずですが、カタログスペックで焦点距離500mmとか言われてもわからんわけです。
で、それを(ある程度)まじめに考えようというのが今回の趣旨です。当然、計算を使いますので知りたい人は我慢して読んでください(笑
といっても、中学レベルの算数・理科の知識があれば十分にわかると思いますので是非。
なお、話を簡単にするために簡略化したり誤魔化した部分もあります。ご了承ください。概ねあっているはずですが、間違いがあっても責任は負いません(免責)。
計算のために
前提条件
以下のワードを使って進めますので、これらがわからない人はちょっとググってみてください。優しい人がたくさん解説してくれています。
- マスターレンズの焦点距離(\(f_{ML}\))
- 最大撮影倍率(\(\beta \) )
- 最短撮影距離(\(L_{min}\))
- ワーキングディスタンス(以下、\(WD\))
- クローズアップレンズの焦点距離(\(f_{CL}\))
- 主点(*後述)
自分の手持ちのレンズで計算してみたい人は、最大撮影倍率、最短撮影距離、WD、クローズアップレンズの焦点距離の数値を用意してください。最大撮影倍率と最短撮影距離はカタログの仕様表にあると思います。W.D.は実測するか、W.D.= (最短撮影距離)-(レンズ全長)-(そのマウントのフランジバック)でも計算できます。
また、意外にもマスターレンズのカタログスペック上の焦点距離は不要です。
用語説明:主点
これだけはここで説明しておきます。すごく大雑把に言うと
- そのレンズを代表する1点。
- その場所にそのレンズと同じ焦点距離の薄いレンズを置いたと思ってよい。
レンズの光学的な重心位置とでもいえばよいでしょうか。複雑な形の物体があったとしても、計算上は重心にその重さのものがあると扱ってもよいのと同じように、何枚もの複雑なレンズがあったとしても主点にレンズがあるとして扱ってもよいということです。
計算してみる!
計算に使う数値(例)
今回は以下の数値を例にして計算してみます。
- 最大撮影倍率(\(\beta \) ) : 0.2倍
- 最短撮影距離(\(L_{min}\)) : 300mm
- WD (\(WD\)) : 230mm
- クローズアップレンズ焦点距離(\(f_{CL}\)) :200mm
ちなみに、上記の数値はLumix 42.5mm/f1.7に近い値です。
マスターレンズの焦点距離は不要です。フォーカシングで変化してしまうことが多いからです。インナーフォーカス式のレンズや、フローティングなどが該当します。
レンズ単体でのフォーカシング時の状態
まずはこちらの図を見てください。手書きで字も絵も汚いのはご勘弁を。
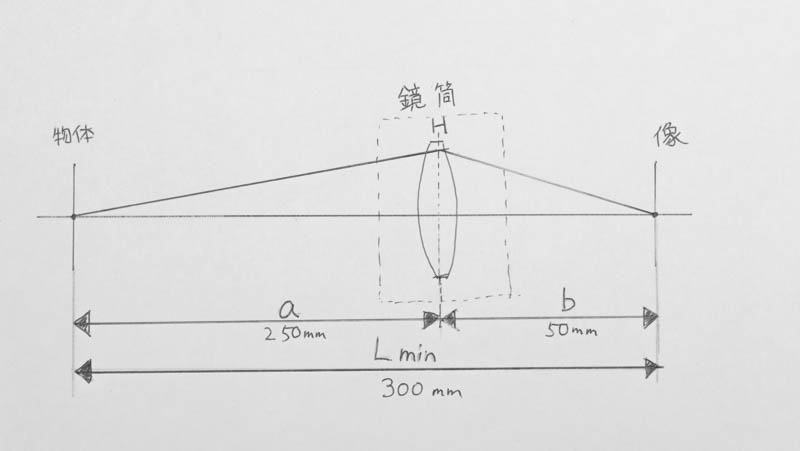
レンズ鏡筒と、主点がありますね。望遠系のレンズだと主点の位置は鏡筒よりも物体側にあることが多いですが、今回は鏡筒の中に主点を書いています。これをHとします。
また、物体面から像面までの距離が最短撮影距離300mm、物体から主点までをa、主点から像面までをbとしています。また、最大撮影倍率は0.2です。この時次の式が成り立ちます。
\(b/a=0.2\)
\(a+b=300\)
この連立式を解くと\(a=250\)mm,\(b=50\)mmになります。
ここで、中学校で習うレンズの公式\(1/a+1/b=1/f \)を使って、最大撮影倍率における焦点距離\(f’_{ml}\)が計算できます。
\(f’_{ml}=41.67\)mm
また、\(WD=230\)mmとしましたので、レンズ鏡筒先端から主点までの距離\(d\)は
\(d=250-230=20\)mm
となります。
クローズアップレンズを装着
次に、クローズアップレンズを装着した場合を考えます。縮尺がおかしいですが(以下略
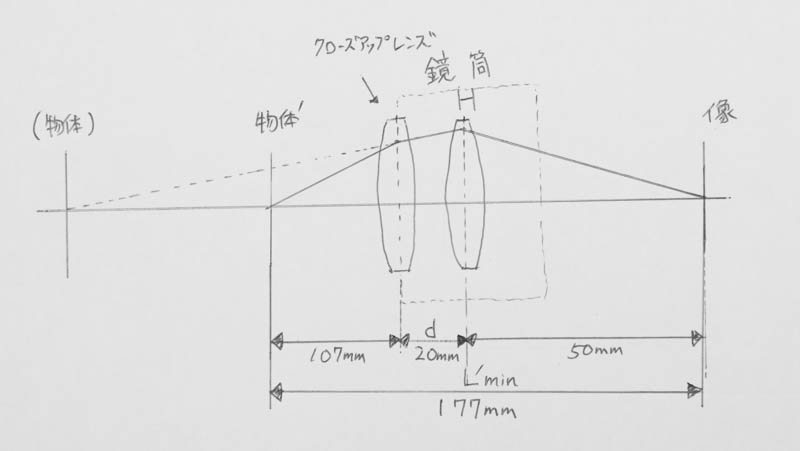
クローズアップレンズは鏡筒先端に取り付けますので、クローズアップレンズとマスターレンズの距離は\(d=20\)mmです。このときの合成焦点距離は、クローズアップレンズの焦点距離\(f_{CL}\)、マスターレンズのフォーカシング時の焦点距離\(f’_{ML}\)’を使って
\(\displaystyle f’=\frac{f_{CL}f’_{ML}}{f_{CL}+f’_{ML}-d}=\frac{200*41.67}{200+41.67-20}=37.6\)mm
となります。このときのワーキングディスタンス\(WD’\)は、レンズの公式を使って
\(\displaystyle \frac{1}{WD}+\frac{1}{WD’}=\frac{1}{f_{CL}}\)
を解いて、\(WD’=107\)mmとなります。
仕上げ
ここまでで、クローズアップレンズを装着した時のワーキングディスタンスと焦点距離が計算できました。図を簡単にするために、今は2つのレンズで表していますが、これを1つの薄いレンズで置き換えて考えます。
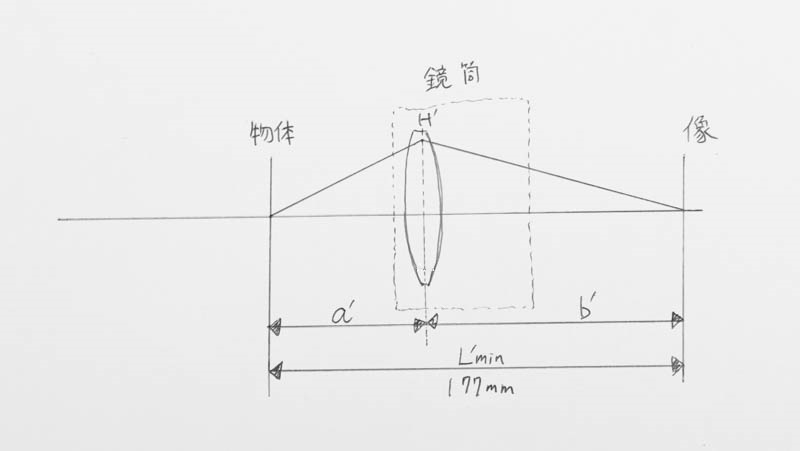
レンズの公式から\(1/a’+1/b’=1/f’ \)ですよね。また、\(a’+b’=L’_{min}=177\)です。
\(a’\)か\(b’\)の2次方程式になりますので答えは2組でてきます。2次方程式の解の公式を使えばOKです。
\((a’,b’)=(54.19,122.81) or (122.81,54.19)\)
ここで、\(WD’\)が\(107\)mmですので、\(a’=54.19\)というのはありえないはず(※)なので
\((a’,b’)=(122.81,54.19)\)
が正解で、このときの撮影倍率は\(b’/a’=0.44\)倍です。
計算結果のまとめ
+
クローズアップレンズNo.5 \(f=200\)mm
=
最短撮影距離\(177\)mm,最大撮影倍率 \(0.44\)倍,ワーキングディスタンス\(=107\)mm
ということがわかりました。
実写で確認
Lumix G 42.5mmf1.7で確認をしてみました。左図がレンズ単体での最至近で撮影したもの、右図がNo.5のクローズアップレンズを使用して最至近で撮影したものです。


目分量ですが撮影倍率は概ね2倍強になっていて計算結果と一致していることがわかります。(※撮影倍率そのものが2倍強という意味ではなく、クローズアップレンズの装着によって撮影倍率の数字が、計算結果と同様に倍になった、という意味です。日本語難しい。)
まとめ
いかがだったでしょうか。ちょこちょことゴマかしながら書いたのでおかしな点もあったかと思いますが、この手順で計算すれば自分のレンズとクローズアップレンズを組み合わせた場合にどのような撮影ができるか(どのようなスペックになるか)イメージができると思います。
で、これでも面倒だと思いますので近々計算用のツールを公開する予定です。
->計算ツールを公開しました。


コメント